Experiment: N-Way Split Karatsuba

January 20th, 2019

While looking for sane1 FFT-like bignum multiplication algorithms, I stumbled upon an equation for N-way-split Karatsuba multiplication algorithm. I got interested and proceeded to implement it.

Consider a task of multiplying two bignums, U and V, split into N equal parts (which may or may not coincide with the bignum limbs), each part of ω bits. Then, the equation that describes schoolbook multiplication is2:
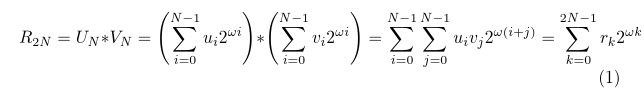
R_{2N} = U_N*V_N = \left( \sum_{i=0}^{N-1}u_i 2^{\omega i} \right) * \left( \sum_{i=0}^{N-1}v_i 2^{\omega i} \right) = \sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_j 2^{\omega(i+j)} = \sum_{k=0}^{2N-1}r_k 2^{\omega k}
Here, N is the number of limbs.

Now, lets have a look at the N-way-split Karatsuba:
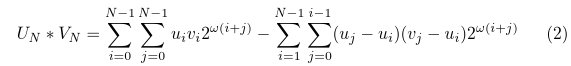
U_N*V_N = \sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_i 2^{\omega(i+j)} - \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j-u_i)(v_j-u_i)2^{\omega(i+j)}

Does it really work? Let's have a look. Let's expand the expression in the second sum in the equation:
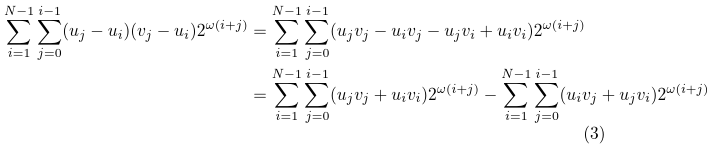
\sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j-u_i)(v_j-u_i)2^{\omega(i+j)} &= \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j v_j - u_i v_j - u_j v_i + u_i v_i)2^{\omega(i+j)}\\ &= \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j v_j + u_i v_i)2^{\omega(i+j)} - \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_i v_j + u_j v_i)2^{\omega(i+j)}
Each of these sums can be further simplified. I'll use the second one as an example:
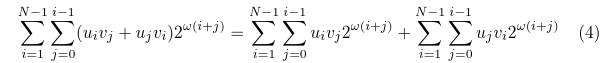
\sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_i v_j + u_j v_i)2^{\omega(i+j)} = \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}u_i v_j2^{\omega(i+j)} + \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}u_j v_i2^{\omega(i+j)}
Let's change the summation order in the second sum, and then rename the indices:
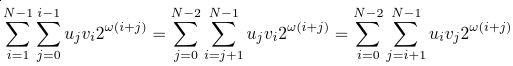
\sum_{i=1}^{N-1}\sum_{j=0}^{i-1}u_j v_i 2^{\omega(i+j)} = \sum_{j=0}^{N-2}\sum_{i=j+1}^{N-1}u_j v_i 2^{\omega(i+j)} = \sum_{i=0}^{N-2}\sum_{j=i+1}^{N-1}u_i v_j2^{\omega(i+j)}
Now, plug this sum back into the equation (4), we can see that we can unite the domains of both sums:
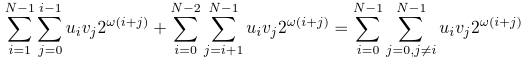
\sum_{i=1}^{N-1}\sum_{j=0}^{i-1}u_i v_j2^{\omega(i+j)} + \sum_{i=0}^{N-2}\sum_{j=i+1}^{N-1}u_i v_j2^{\omega(i+j)} = \sum_{i=0}^{N-1}\sum_{j=0, j \neq i}^{N-1}u_i v_j2^{\omega(i+j)}
Exactly same transformations can be done for the first sum in equation (3):
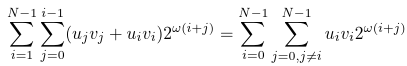
\sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j v_j + u_i v_i)2^{\omega(i+j)} = \sum_{i=0}^{N-1}\sum_{j=0, j \neq i}^{N-1}u_i v_i2^{\omega(i+j)}
Let's return to equations (2) and (1):
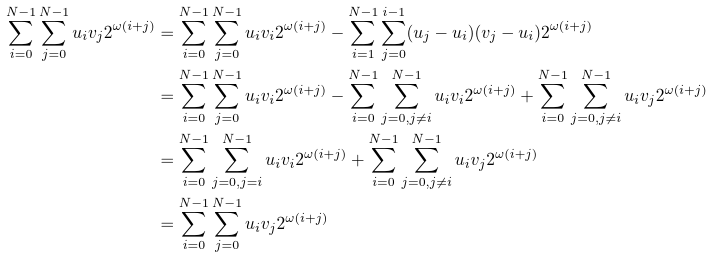
\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_j 2^{\omega(i+j)} &= \sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_i 2^{\omega(i+j)} - \sum_{i=1}^{N-1}\sum_{j=0}^{i-1}(u_j-u_i)(v_j-u_i)2^{\omega(i+j)}\\ &=\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_i 2^{\omega(i+j)} - \sum_{i=0}^{N-1}\sum_{j=0, j \neq i}^{N-1}u_i v_i2^{\omega(i+j)} + \sum_{i=0}^{N-1}\sum_{j = 0, j\neq i}^{N-1}u_i v_j2^{\omega(i+j)}\\ &=\sum_{i=0}^{N-1}\sum_{j=0, j = i}^{N-1}u_i v_i2^{\omega(i+j)} + \sum_{i=0}^{N-1}\sum_{j = 0, j\neq i}^{N-1}u_i v_j2^{\omega(i+j)}\\ &=\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}u_i v_j 2^{\omega(i+j)}
Q.E.D.

Implementing this equation directly as two sums over one working register would be impractical, so equation (2) can be further rewritten as:
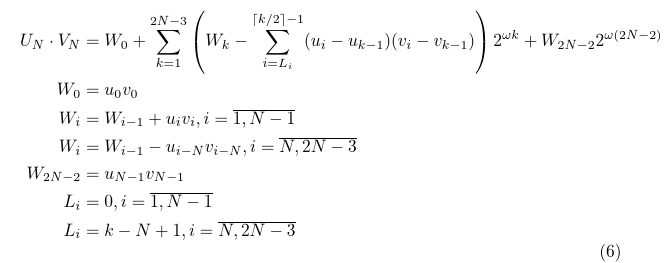
U_N\cdot V_N &= W_0 + \sum_{k=1}^{2N-3}\left(W_k - \sum_{i=L}^{\lceil k/2 \rceil-1}(u_i-u_{k-1})(v_i-v_{k-1})\right)2^{\omega k} + W_{2N-2}2^{\omega(2N-2)} \\ W_0 &=u_0 v_0\\ W_i &=W_{i-1} + u_i v_i, i= \overline{1,N-1} \\ W_i &=W_{i-1} - u_{i-N} v_{i-N}, i= \overline{N,2N-3} \\ W_{2N-2} &= u_{N-1} v_{N-1}\\ L_i &=0, i= \overline{1,N-1} \\ L_i &=k-N+1, i= \overline{N,2N-3}
I did no proofs in this transformation, which I mostly got from the original publication3. The reason is that the performance of this algorithm is around two times lower than the performance of FFA Ch. 10 algorithm, so the value of such proof would be purely educational.

So, let's have a look at the code. For calculating the (uj-ui)(vj-ui) terms, I used the same method as Stanislav did, but calculating an absolute difference of two Words rather than two FZs. Addition to words_ops.ads:

   procedure Word_Sub_Abs(X: Word;
                          Y: Word;
                          Diff: out Word;
                          Underflow: out WBool);

And to word_ops.adb:

   procedure Word_Sub_Abs(X: Word;
                          Y: Word;
                          Diff: out Word;
                          Underflow: out WBool) is
   begin
      Diff := X - Y;
      Underflow := W_Borrow(X, Y, Diff);
      Diff := Diff xor (0 - Underflow);
      Diff := Diff + Underflow;
   end Word_Sub_Abs;

The rather draft-quality Ada code for multiplication algorithm follows. I did not precompute the uivi products, because the performance is even lower with such precomputation.

   -- Karatsuba's N-Way-Split Multiplier. (CAUTION: UNBUFFERED)
   procedure Mul_Karatsuba(X  : in  FZ;
                           Y  : in  FZ;
                           XY : out FZ) is

      -- L is the wordness of a multiplicand. Guaranteed to be a power of two.
      L : constant Word_Count := X'Length;

      -- A result of multiplication of two words.
      subtype DWord is FZ(1 .. 2);

      -- Subtraction borrows, signs of (XL - XH) and (YL - YH),
      Cx, Cy     : WBool; -- so that we can calculate (-1^DD_Sub)

      -- Words for calculating the difference:
      DX: Word;
      DY: Word;

      -- Whether the DD term is being subtracted.
      Sub     : WBool;

      -- Carry from individual term additions.
      C          : WBool;

      -- Carry accumulator
      TC         : Word := 0;

      -- Barring a cosmic ray, the tail ripple will NOT overflow.
      FinalCarry : WZeroOrDie := 0;

      -- Multiplication result
      XY_K: DWord;

      -- W Component of a sum
      W : DWord := (others => 0);
      TC_W : Word := 0;

      First_DWord : DWord renames XY(XY'First .. XY'First + 1);
      Last_DWord : DWord renames XY(XY'Last - 1 .. XY'Last);
   begin
      -- Calculate W_0
      XY(XY'Range) := (others => 0);
      Mul_Word(X => X(X'First), Y => Y(Y'First),
               XY_LW => First_DWord(1), XY_HW => First_DWord(2));
      W := First_DWord;
      -- TC_W stays equal to zero;

      -- First half of XY
      for K in 1 .. L - 1 loop
         declare
            RSeg : DWord renames XY(XY'First + K .. XY'First + K + 1);
         begin
            -- Calculate W_k based on W_{k-1}
            Mul_Word(X => X(X'First + K), Y => Y(Y'First + K),
                     XY_LW => XY_K(1), XY_HW => XY_K(2));
            FZ_Add_D(X => W, Y => XY_K, Overflow => C);
            TC_W := TC_W + C;
            -- Add W_k to Result
            FZ_Add_D(X => RSeg, Y => W, Overflow => C);
            TC := TC_W + C;

            for I in 0 .. (K + 1)/2 - 1 loop
               Word_Sub_Abs(X(X'First + I), X(X'First + K - I), DX, CX);
               Word_Sub_Abs(Y(Y'First + I), Y(Y'First + K - I), DY, CY);
               Mul_Word(DX, DY, XY_K(1), XY_K(2));
               Sub := 1 - (CX xor CY);
               FZ_Not_Cond_D(N => XY_K, Cond => Sub);
               FZ_Add_D(OF_In => Sub, X => RSeg, Y => XY_K, Overflow => C);
               TC := TC + C - Sub;
            end loop;

            XY(XY'First + K + 2) := TC;
         end;
      end loop;

      -- Second half of XY
      for K in L .. 2*L - 3 loop
         declare
            RSeg : DWord renames XY(XY'First + K .. XY'First + K + 1);
         begin
            -- Calculate W_k based on W_{k-1}
            Mul_Word(X => X(X'First + K - L), Y => Y(Y'First + K - L),
                     XY_LW => XY_K(1), XY_HW => XY_K(2));
            FZ_Sub_D(X => W, Y => XY_K, Underflow => C);
            TC_W := TC_W - C;
            -- Add W_k to Result
            FZ_Add_D(X => RSeg, Y => W, Overflow => C);
            TC := TC_W + C;

            for I in (1 + K - L) .. (K + 1)/2 - 1 loop
               Word_Sub_Abs(X(X'First + I), X(X'First + K - I), DX, CX);
               Word_Sub_Abs(Y(Y'First + I), Y(Y'First + K - I), DY, CY);
               Mul_Word(DX, DY, XY_K(1), XY_K(2));
               Sub := 1 - (CX xor CY);
               FZ_Not_Cond_D(N => XY_K, Cond => Sub);
               FZ_Add_D(OF_In => Sub, X => RSeg, Y => XY_K, Overflow => C);
               TC := TC + C - Sub;
            end loop;

            XY(XY'First + K + 2) := TC;
         end;
      end loop;

      -- Last word
      Mul_Word(X(X'Last), Y(Y'Last), XY_K(1), XY_K(2));
      FZ_Add_D(X => Last_DWord, Y => XY_K, Overflow => FinalCarry);
      pragma Assert(FinalCarry = 0);
   end Mul_Karatsuba;
   -- CAUTION: Inlining prohibited for Mul_Karatsuba !

How does this code perform, and why? As a simple benchmark I used 2048.tape. The performance sucks:

# Original FFA
$ perf stat -d -- ./ffa_calc 4096 32 < 2048.tape

 Performance counter stats for './ffa_calc 4096 32':              

        813.185246      task-clock (msec)         #    0.999 CPUs utilized
                10      context-switches          #    0.012 K/sec
                 0      cpu-migrations            #    0.000 K/sec
                26      page-faults               #    0.032 K/sec
     2,917,709,084      cycles                    #    3.588 GHz
    10,217,779,596      instructions              #    3.50  insn per cycle
     1,583,047,981      branches                  # 1946.725 M/sec
           510,722      branch-misses             #    0.03% of all branches
     1,448,360,271      L1-dcache-loads           # 1781.095 M/sec
            58,482      L1-dcache-load-misses     #    0.00% of all L1-dcache hits
             5,155      LLC-loads                 #    0.006 M/sec
               877      LLC-load-misses           #   17.01% of all LL-cache hits

       0.813790434 seconds time elapsed
# FFA with n-way-split
$ perf stat -d -- ./ffa_calc_k 4096 32 < 2048.tape

 Performance counter stats for './ffa_calc_k 4096 32':

       1548.798929      task-clock (msec)         #    1.000 CPUs utilized
                 9      context-switches          #    0.006 K/sec
                 0      cpu-migrations            #    0.000 K/sec
                24      page-faults               #    0.015 K/sec
     5,678,373,211      cycles                    #    3.666 GHz
    19,929,356,644      instructions              #    3.51  insn per cycle
     3,251,337,471      branches                  # 2099.264 M/sec
        17,148,781      branch-misses             #    0.53% of all branches
     3,495,601,406      L1-dcache-loads           # 2256.976 M/sec
            32,558      L1-dcache-load-misses     #    0.00% of all L1-dcache hits
             6,265      LLC-loads                 #    0.004 M/sec
               957      LLC-load-misses           #   15.28% of all LL-cache hits

       1.549368721 seconds time elapsed

It is immediately clear that there is much more instructions executed in the N-Way-Split variant, and, accordingly much more memory loads. So it's not clear to me how to proceed from here. Using Comba's algorithm may return some of the performance, but the code is gnarly enough as it is, to complicate it even more4.

I would consider adding the missing proofs and reworking this code in the future, but first would like to hear some comments from more knowledgeable people what improvement can be made, and whether it's worth spending time on this code at all. As for me, I'm quite satisfied already with understanding math behind it.

  1. First and foremost, no floating point. [↩]
  2. Given that HTML sucks for displaying math, I rendered all equations to images, latex document here. [↩]
  3. I did have to fix one mistake in the equation there (pdf), so it still needs to be taken with a grain of salt [↩]
  4. Which makes me also very sceptical about performance of more complex multiplication algorithms. [↩]

Posted in Ada | 2 Comments »

« Older Entries
Newer Entries »